Nicolas, rédacteur chez Interpost, a travaillé cet hiver chez GEONAUTE, la marque de course d’orientation de Décathlon. Il était spécialisé sur la gamme des boussoles en tant qu’ingénieur produit. Dans cette série de deux articles réalisée en partenariat avec GEONAUTE, il nous éclaire sur le fonctionnement, pas aussi simple qu’il n’y paraît, des boussoles de course d’orientation.
Ce deuxième article explique plus en détail la modélisation et les tests mis en place pour améliorer les performances des boussoles. Il est nécessaire d’avoir lu le premier article de la série pour bien comprendre les phénomènes mis en jeu et les termes utilisés.

Forts de toutes ces connaissances sur le fonctionnement de la boussole, il nous faut maintenant déterminer quels sont les paramètres qui influent sur l’équilibrage, la stabilité et la rapidité. Il faut aussi déterminer quelles sont les valeurs optimales de ces paramètres, ou à défaut le meilleur compromis entre tous ces paramètres. Pour cela, il y a deux approches possibles :
-
L’expérimentation : on met en place des tests sur banc d’essai pour mesurer équilibrage, stabilité et rapidité.
-
La modélisation : on écrit les équations qui régissent la dynamique de l’aiguille de la boussole et on fait des expériences virtuelles.
En réalité, les deux approches sont indispensables : la modélisation permet de comprendre en profondeur les phénomènes impliqués, et l’expérimentation permet de vérifier si les résultats de la modélisation correspondent à la réalité.
L’équilibrage
Pour un rappel sur la notion d’équilibrage d’une boussole : L’équilibrage.

Mesure expérimentale de l’équilibrage
Comme le décalage de l’aimant par rapport au centre de l’aiguille est toujours inférieur au millimètre, il est très difficile de le mesurer précisément. Il est cependant facile de mesurer l’erreur de l’aiguille par rapport au nord si la boussole est penchée d’un certain angle par rapport à l’horizontale.
Pour cela on utilise un banc d’essai très simple. Comme tous ceux relatifs aux boussoles, il est entièrement en bois pour ne pas perturber le champ magnétique terrestre local (ou alors les éléments métalliques sont situés à distance suffisante de la boussole). Il est constitué d’un socle sur lequel est fixé un plateau pivotable par rapport à un axe horizontal. Deux rapporteurs permettent de relever :
-
L’angle d’inclinaison du plateau pivotable
-
L’angle d’erreur de l’aiguille par rapport au nord.
Le plateau est mis en position horizontale, la boussole est fixée dessus et le banc est orienté au nord. Les deux rapporteurs indiquent donc 0°. On fait ensuite varier l’inclinaison du plateau, et on relève l’erreur de l’aiguille par rapport au nord.

Modélisation de l’équilibrage
La modélisation de la boussole permet d’obtenir l’expression du décalage du centre de gravité de l’aimant pour qu’elle soit parfaitement équilibrée pour une position donnée sur le globe terrestre.
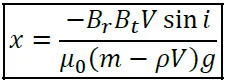
L’index des notations est disponible en bas de cet article.
La modélisation permet aussi de calculer l’angle d’erreur que fait l’aiguille par rapport au nord si la boussole est penchée d’un certain angle par rapport à l’horizontale (avec comme axe de rotation celui indiqué par l’aiguille lorsque la boussole est posée parfaitement à plat).
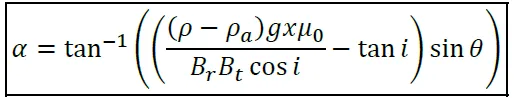
L’index des notations est disponible en bas de cet article.
La stabilité
Pour un rappel sur la notion de stabilité d’une boussole : La stabilité.
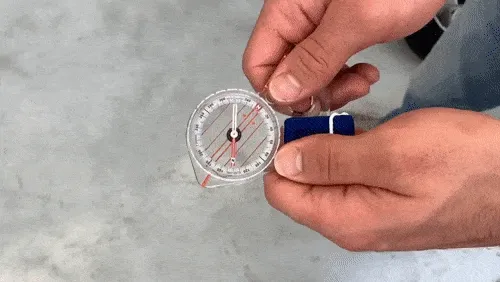
Mesure expérimentale de la stabilité
La stabilité de l’aiguille peut encore une fois être mesurée grâce à un banc d’essai. Le but est d’appliquer une oscillation latérale à la boussole tout en mesurant l’amplitude des oscillations de l’aiguille. Le banc est constitué de deux ensembles :
-
Un chariot sur lequel est fixée la boussole, et une caméra qui permet de la filmer pendant l’expérience.
-
Un dispositif “bielle manivelle” qui applique les oscillations au chariot.
La manivelle est entraînée en rotation par un moteur dont on peut contrôler la fréquence de rotation. On mesure l’amplitude des oscillations de l’aiguille avec la caméra.

Modélisation de la stabilité
La modélisation permet de prédire la cinématique de l’aiguille lorsque l’on applique des oscillations de type “course à pied” à la boussole. Pour simplifier le problème, on ne prend en compte que les oscillations latérales par rapport au nord (ce qui correspond au cas le plus contraignant en termes de stabilité, à cause du décalage de l’aimant).
On obtient une jolie équation différentielle du second ordre :
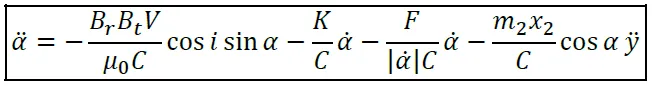
L’index des notations est disponible en bas de cet article.
On peut utiliser cette équation pour modéliser numériquement le test de stabilité sur un ordinateur. Cela permet de comparer le résultat à celui observé sur le banc d’essai.
La rapidité
Pour un rappel sur la notion de rapidité d’une boussole : La rapidité.

Mesure expérimentale de la rapidité
Le test de rapidité consiste à maintenir l’aiguille de la boussole à 90° par rapport au nord (à l’aide d’un électroaimant), puis à la relâcher et à mesurer le temps mis pour revenir à sa position d’équilibre.
L’aiguille est filmée selon une vue de dessus, ce qui permet de récupérer sa position angulaire avec un logiciel de pointage vidéo.

Modélisation de la rapidité
La modélisation permet de prédire la cinématique de l’aiguille lorsqu’on la lâche d’un angle de 90 degrés par rapport au nord. Pour obtenir l’équation, c’est très simple : il suffit de retirer le terme en y (correspondant aux oscillations horizontales) de l’équation précédente.

L’index des notations est disponible en bas de cet article.
Conclusion
Alors, me direz-vous, avec toute cette artillerie, rien de plus facile que de concevoir la boussole idéale ?
Rappelez-vous : quand on parle de boussoles, tout est dans le compromis. Une boussole parfaitement équilibrée sera moins stable, et l’amélioration de la rapidité se fait aussi aux dépens de la stabilité.
Tous ces (magnifiques) bancs d’essai et toutes ces équations sont des outils très utiles pour affiner les paramètres influant sur les performances de la boussole, mais au final ce sont les préférences des utilisateurs qui permettront de trouver les bons compromis.
Pendant le processus de conception, il faut donc obligatoirement passer par des tests sur le terrain !
Index des notations
